旺文社
教育情報センター

Educational Information Center

 

 

　日本数学会に所属する約5,000名の大学教員の間では、ちょうどセンター試験が開始された平成2(1990 )年頃から、新入生の数学の学力低下が指摘されていたという。それを受け、同学会が8年(1996)年に大学教員を対象にしたアンケート調査の結果、ごく基本的な能力が学生の間で低下しつつあるという現実が浮き彫りにされた。
　その後も同学会では、より広汎な数学教育全般について調査・提言を行ってきたが、学生の学力低下は深刻化し、12(2000)年頃には多くの大学で高校数学の補習授業(リメディアル教育)が必要になったという。特にここ数年は多くの会員から、「入学試験や1年生の期末試験における数学の答案にまったく意味の通じないものが増え、どう対処したらよいか当惑している」などの声が寄せられているという。
　こうした経緯と教育現場に広がっている危惧を踏まえ、「大学生数学基本調査」(以下、「基本調査」)を実施したという。

 

●　調査実施時期：23年4月1月～7月20日
●　調査実施大学：国公私立48大学(オリエンテーション等を含む90クラス)
●　調査を受けた学生数：5,934人
 

◆　大学、学部・学科系統の分類
　「基本調査」では、調査実施大学及び調査を受けた学生が主として所属する学部・学科を次のように分類している。
●　大学群：国公立大と私立大とに2分したうえで、各大学の一般入試の合格難易度を基にして、難易度上位順に、次のような国公立大3群、私立大4群に分類している。
［国公立大］
・国立大Ｓ群(学生数1,041人、調査受検者に対する割合17.5％)
・国公立大Ａ群(同2,203人、37.1％) ／・国公立大Ｂ群(同698人、11.8％)
［私立大］
・私立大Ｓ群(同230人、3.9％)／　・私立大Ａ群(同823人、13.9％)
・私立大Ｂ群(同596人、10.0％)／・私立大Ｃ群(同343人、5.8％)
●　学部・学科系統
・理工系(理学、工学系統。学生数2,502人、調査受検者に対する割合42.2％)
・文学系(文学、外国語系統。同202人、3.4％)
・社会科学系(法学、経済･経営･商学、社会学、国際関係学系統｡同853人､14.4％)
・教育系(教員養成、教育学系統。同1,179人、19.9％)
・保健衛生系(医学、歯学、薬学、保健衛生学系統。同391人、6.6％)
・学際系(学際系統。同251人、4.2％)
・混合(同530人、8.9％)
　＊注．｢混合｣は複数系統の混合クラスのため､分類ができないもの。なお､農林水産・生活科学・芸術系等はサンプル数が少ないため系統別の分類には含まれていない。
◆　問題数、出題内容・範囲等
　出題問題は、「第1ステージ：問1－1、問1－2」(大問2題：解答時間5分)／「第2ステージ：問2－1、問2－2」(大問2題：同10分)／「第3ステージ：問3」(大問1題：同10分)の3つのステージ(大問5題)からなる。
　「第1ステージ｣ (問1)は文章に含まれる論理の的確な読み取り、「第2ステージ」(問2)は論理的に正しい記述、「第3ステージ」(問3)は相似を利用した作図(記述)についてのそれぞれ出題である。
　また、問題解答に先立ち、小・中・高校での得意・不得意科目、塾・予備校等での算数・数学の学習経験、大学入試での数学受験の有無、センター試験などマークシート方式のみの受験か、数学の記述試験を受験したかを問うアンケート調査(5分程度)も実施。
◆　出題範囲等
　今回の調査受検者が学んだ旧課程の高校学習指導要領(数学は24年度から新課程で先行実施)では、「数学Ｉまたは数学基礎」(選択必履修)以外は必履修から外れており、また、大学入試科目(センター試験科目を含む)において、数学を必須科目としない大学・学部が私立大文系を中心に多くみられる。
　こうしたことから、日本数学会では「基本調査」の出題範囲を小・中学校及び数学Ｉのごく基礎的な範囲に留めたとしている。
　今回の調査受検者は旧課程の小・中・高校学習指導要領で算数・数学を学習してきた。各問題の出題内容／問題形式／及び出題内容が学習指導要領(旧課程)で最初に扱われる学年は、それぞれ下記のとおりである。なお、小・中学校の算数・数学は21年度から、高校の数学は24年度から新課程で先行実施されている。
・問1－1：平均の定義とそれに関する初歩的な推論／選択式／小学6年
・問1－2：命題と条件の論理的な読み取り／選択式／特定されない (小学校～高校まで各学校段階を通じて学習)
・問2－1：整数の性質に関する初歩的な論証／記述式／中学2年
・問2－2：二次関数の性質の列挙／記述式／高校1年
・問3：平面図形と相似を利用した作図／記述式／中学3年

 

 

「基本調査」の設問は、次のとおり。解答欄は省略し、正答例(日本数学会公表)は後掲。

 

 

［第１ステージ］
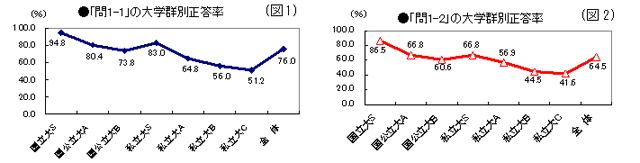
◆問1－1：(図1参照)
・「平均の定義と基本的な性質の認識」の正答率は76.0%で、調査受検者5,934人の大学生“4人に1人”が、平均の意味を正しく理解していないことになる。大学群別の正答率では、国立大S群(正答率94.8％。以下、同)と国公立大A群(80.4％)が8割以上の高い正答率であるが、私立大B群(56.0％)・私立大C群(51.2％)ではほぼ半数の学生が不正解である。
・正答率の高い国立大S群・国公立大A群は、アンケート調査から、数学記述試験経験あり／小・中学校での算数・数学得意／物理得意、といったグループであるという。
　一方、正答率が高くない私立大A群・私立大B群・私立大C群は、数学記述試験経験なし／小・中学校での算数・数学がともに不得意または普通／物理不得意、のグループだったという。
・学部・学科系統別の正答率では、社会科学系が82.6％で、理工系の82.0％をわずかに上回っているのが注目される。理工系は“平均値の算出”(計算)はできても、“平均の正しい理解”は、「経済･経営･商学」系の学生を主体に社会科学系のほうがやや上回っていることなどが伺える。
・旧課程における「平均」についての学習は、まず小学6年の「数量関係」の領域で学んでいる。そして、「数量」の変量を“ならす”「相加平均」(変量の値の総和÷全個数)についての意味は多くの子どもたちが理解し、日常的に使っているとみられる。ただ、今回の「基本調査」で、たとえ「平均値」(相加平均)は算出できるとしても、「平均の定義と問題文からの推論」が十分身についていないことが伺える。なお、「資料」全体の分布の様子や特徴をみる「中央値」、「ヒストグラム」は、新課程の中学1年で扱われている。
◆問1－2：(図2参照)
・「文の論理的読解」の正答率は全体で64.5％。日本数学会では、調査対象となった大学生“3人に1人”が論理的読解に課題があるとしている。大学群別の正答率では、国立大S群(86.5％)を除き、すべての大学群で70%を下回り、特に私立大B群・私立大C群では5割を割っている。
・当問題は、問題文の内容から、設問の記述の“真偽”を判定する「論理的思考力」をみるもので、「集合」に関する出題でもある。このような読解力(論理的思考力)は、小学校から高校までの各学校段階に応じ、算数・数学の題材等を通して培われる。
　◎　日本数学会の総合分析
　｢平均の定義と、定義から導かれる初歩的結論｣(問1－1)、｢少し複雑な命題の論理的読み取り｣(問1－2)のどちらも誤答率が高く、論理を正確に解釈する能力に問題があることを示している。

 

 

［第２ステージ］
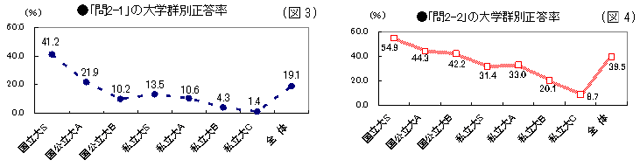
◆問2－1：(図3参照)
・「偶数＋奇数は奇数になることの論証」の正答率は、全体で19.1%と低い。国立大S群(41.2％)と他の大学群(国公立大A群＜21.9％＞～私立大C群＜1.4％＞）の二極化が目立つ。
・中学校(旧課程)では、整数の性質について文字を使って説明することを学んだ。特に、「3つの連続する整数の和が3の倍数になること」の論証などは、高校入試でも頻出問題。
・因みに、文科省の中3生対象の｢平成22年度全国学力・学習状況調査｣では、｢連続する3つ、及び４つの奇数の和｣について出題され(B問題の大問２　)、｢連続する3つの奇数の和が3の倍数になる」論証問題の正答率は“26.4%”であった(私立大の全ての大学群より高い正答率)。
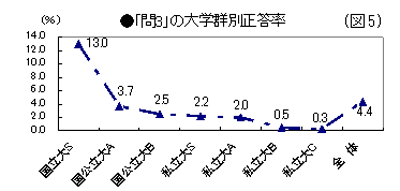
◆問2－2：(図4参照)
・「二次関数のグラフの性質」の全体の正答率は、39.5%である。
・大学群別の正答率は、国立大S群(54.9％)を除き、全ての大学群で5割を割っている。
　ただ、“正答＋準正答率”をみると、大学群は次のような4グループに分かれるという。
　①国立大S群＝“正答＋準正答率”(約75％)が圧倒的に多い。／②国公立大A群・国公立大B群＝“正答＋準正答”(約60％～54％)が半数を超え、重篤な誤答が少ない。／③私立大S群・私立大A群＝“正答＋準正答率”(約45％～約43％)が5割以下で、誤答が半数を超え、重篤な誤答もかなりいる。／④私立大B群・私立大C群＝“正答＋準正答率”(約28％～約12％)が低く､誤答が圧倒的に多い。理工系の正答率“48.4％”の低さも懸念される。
・日本数学会は、「“変化する2つの値の関係”を数量的に捉えることは、科学的に世界を理解するうえで、欠くことができない最も基本的な方法論である」としている。
◎　日本数学会の総合分析
　記述式の入試を課している国立難関大の合格者を除くと、｢偶数と奇数の和が奇数になる｣ (問2－1)証明を明快に記述できる学生は稀である。
　また、二次関数の性質を列挙する問題(問2－2)では、意味不明の解答が多く、準正答のなかにも、すでに挙げた性質と重複する性質を再度挙げる解答が目立つ。
　論理を整理された形で記述する力が不足している。

 

 

［第３ステージ］
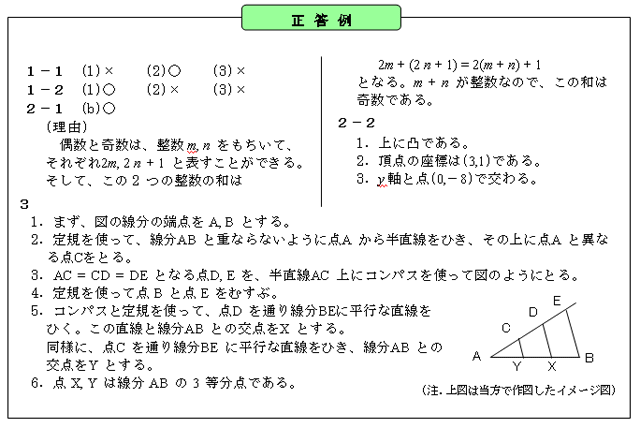
◆問3：(図5参照)
・「相似を利用した作図」の全体の正答率は4.4%と極めて低く、“正答＋準正答率”でも7.6％と、1割を割っている。
　大学群別では国立大S群のみが正答率13.0％で1割を超えているものの、他は4％以下で、特に私立大B群・私立大C群では1％に満たない。なお、理工系の正答率は6.6％で、“正答＋準正答率”でも11.2％と、1割をやや上回る程度である。
・当問題は、相似を利用した問題解決の好例として、ほとんどの中学3年の数学教科書(旧課程)で扱われている。ただ、正答率が極めて低いことから、数学の活用力を伸ばすために用意されている題材が十分活かされていないようだ。
　こうした背景の一つとして、一般に入試における作図問題の出題頻度が低いため、入試対策上、図形の指導や学習が軽減されがちになっていることが指摘されている。
・日本数学会では、「入試では解答時間や形式の制約等があり、どうしても出題されやすい単元や分野に偏りが出る。しかし、多くの教科書が同じ問題(題材)を取り上げていることは、数学の理解を深めるうえで欠くことができない重要な問題として位置付けられているということで、より充実した指導が行われることを期待する」としている。
◎　日本数学会の総合分析
　平面図形を定規とコンパスで作図することが、何を意味するのか理解していない解答が多く見られる。
　高校までの教育で、こうしたことがきちんと教えられていない可能性もある。
【日本数学会からの提言】
　日本数学会では｢基本調査｣で明らかになった問題点を踏まえ､次のように提言している。
●　中等教育機関に対して：充実した数学教育を通じ論理性を育む。証明問題を解かせるなどの方法により、論理の通った文章を書く訓練を行う。
●　大学に対して：数学の入試問題はできるかぎり記述式にする。1年次、2年次の数学教育において、思考整理と論理的記述を学生に体得させる。
【正答例】
　日本数学会が公表した今回の「基本調査」の正答例を以下に紹介する。
　なお、ここに掲載されているのは正答の一例であり、他の解答例もあるとしている。

 

＊　　　　　　　　＊　　　　　　　　＊

 

 

　今回の「基本調査」で、大学生の基礎的な「数学力」に様々な課題のあることが指摘されている。児童・生徒の学習内容や授業時数、履修単位数などは、教育課程の国家的基準(ミニマム・リクワイアメント)である学習指導要領との関わりをみる必要がある。今回の調査受検者は平成10年代に実施されていた所謂「ゆとり教育」の学習指導要領(旧課程)のもと、授業時数や必修単位数の削減の中で小・中・高校教育を受けてきた。
　そこで、彼らが受けた学習指導要領も含め、各時代の学習指導要領の特色や算数・数学の授業時数、必修単位数などの概要をたどってみる。

 

 

　学習指導要領は戦後の新しい学校制度が発足してから今日まで、各時代の教育情勢や社会的要請等を踏まえ、教育課程基準の見直しや学習指導上の改善策に対応して改訂、実施されてきた。小・中学校では昭和22(1947)年度から、高校では昭和23年度から実施され、初期の時代を除き、ほぼ10年おきに改訂されてきた。
　主な改訂としては、小・中学校では昭和26(1951)年の第1回から平成20(2008)年まで7回改訂され、昭和33(1958)年からは文部省(当時)の改正告示から3～4年後に実施されてきた。高校では昭和35(1960)年の第1回から平成21年まで6回改正告示され、告示から数年後に実施されている。

 

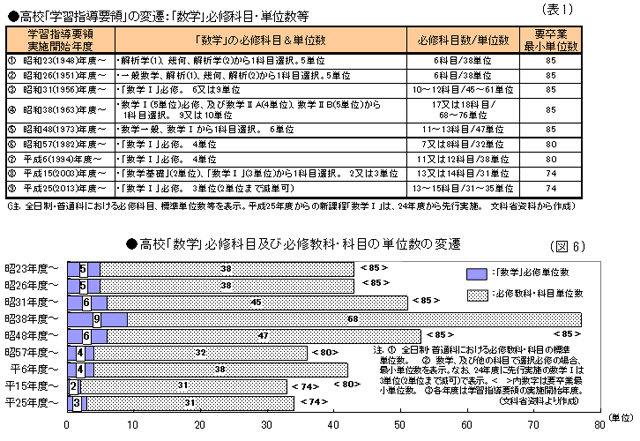
◆　各時代の学習指導要領の特色　(表1、図6・7・8参照)
　学習指導要領(以下、小・中・高校を含め、各時代に実施された学習指導要領)の変遷を概観すると、各時代の学校教育(教育課程)の特色が見て取れる。
１．昭和20年代：新しい学校制度発足当初の昭和20年代は、児童・生徒の生活経験、生活学習に重点を置いた「経験主義」の学習指導要領であった。
２．昭和30年代～40年代：昭和30(1955)年代に入ると、経験主義に基づく児童・生徒中心の教育に対する批判が強まり、学習指導要領は系統的知識の習得を重視する「系統主義」へと転換された。
　さらに、昭和30年代後半になると、当時の高度経済成長を支える人材養成、能力開発政策などの社会情勢と相俟って、学習指導要領は、系統学習の徹底、科学技術教育の向上、授業時数の増加(小学：昭和46年度6,135単位時間、中学：47年度3,535単位時間で過去最高)、高校での必修科目・必履修単位の増加(昭和38年度～47年度：必修単位数68単位、「数学」必修9単位で過去最高)など、「詰め込み教育」路線を強めた。
　その一方、“大学入試の激戦”(「団塊世代」による受験生数激増)、“受験対策、学習量の負担過重”、“落ちこぼれ問題”などで、「詰め込み教育」批判が高まった。
３．昭和50年代：上記のような「詰め込み教育」批判に対し、昭和50(1975)年代の学習指導要領は、個性重視、基礎・基本の習得、教育内容の縮減、必修科目の削減など、所謂「ゆとり教育」へと舵を切った。
４．平成時代初期：平成元(1989)年改訂の学習指導要領では、それまでの“知識・理解重視型学力観”から、「自ら学ぶ意欲の育成や思考力、判断力などの能力の育成に重点を置く」とする“新学力観”への転換を図っている。
５．平成10年代：今回の調査受検者が受けた平成10(1998)年代の学習指導要領は、“ゆとり”の中で「生きる力」(確かな学力／豊かな心／健やかな体)の育成を基本的な理念とする“ゆとり教育の集大成”といえる。
　そして、小・中・高校における14 (2002)年度からの「完全学校週5日制」実施、「総合的な学習の時間」の導入などで、小・中学校では教育内容の3割削減と教科学習の授業時数の大幅削減、高校では必修単位数や要卒業単位数の削減が図られた。
　このため、“ゆとり教育”批判、“学力低下”問題が社会的にも大きな波紋を広げた。
６．平成20年代：上述のように、10年代は“学力低下”論が喧伝される中で教育について“ゆとり”か“詰め込み”か、といった二項対立的な議論がなされてきた。
　こうした経緯を踏まえ、今回の新学習指導要領(小学校23年度、中学校24年度から全面実施、高校25年度から学年進行で実施。小学算数・中学数学は21年度、高校数学は24年度から先行実施)では、これまでの二項対立的な議論を乗り越え(知識・技能とその活用を“車の両輪”として)、「生きる力」の育成を継承している。
　そして“学力の重要な要素”として、①基礎的・基本的な知識・技能の習得／②知識・技能を活用して課題を解決するために必要な思考力・判断力・表現力等／③主体的に学習に取り組む態度、といった3点を挙げている。
　こうした理念に基づき、新学習指導要領では小・中学校の主要教科の授業時数を1割以上増加させるとともに、例えば算数・数学では、言葉や数、式、図表などの相互の関連を正確に理解する論理的思考力、それらを用いて説明、表現する論理的表現力の育成の充実を図っている。

 

 

 

 

　高校生の基礎学力の定着などには、前述したような学習指導要領に則った学校教育のほか、大学入試との関わりも大きく影響している。
　中学生の98.2％(23年度。以下、同)が高校に進学し、高校生(現役)の47.7％が大学(学部)に進学している。なお、18歳(大学進学適齢期)人口に対する既卒者も含めた大学(学部)入学者数の割合、つまり「大学進学率」は51.0％で、“ユニバーサル”段階に達している。
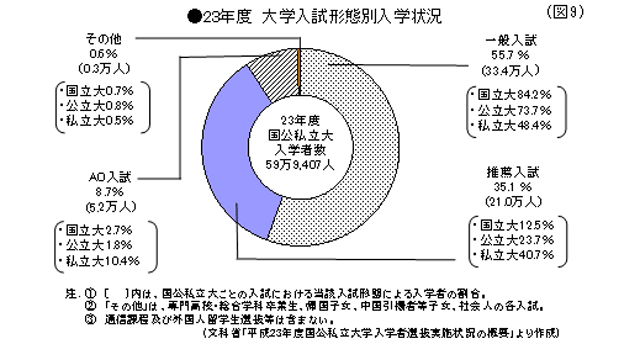
　また、大学入学者約60万人のうち、78.3％に当たる約47万人が私立大生であるが、そのうち“2人に1人”が学科試験を基本的に課さない「推薦・AO入試」によって入学している。(図9参照)
　ところで、大学受験者(現役・既卒)の9割以上が入学を果たす所謂、大学“全入時代”(23年度大学｢収容力｣：90.8％＜大学入学者数÷大学受験者数)＞)とまでいわれる受験環境は、一部の厳しい競争的環境にある受験生を別とすれば、受験生に対してさえも学習意欲の希薄さと学習時間の減少をもたらし、基礎学力の低下を招いているといえる。

 

 

　前述した新学習指導要領では、主要科目の授業時数の増加、理数教育などの教育内容の充実、教科・科目の枠を超えた論理的思考力・表現力の育成の充実、高校教育の多様化に対する共通必履修科目の設定などが図られる。
　一方、大学入試では、中教審答申『学士課程教育の構築に向けて』(20年12月)や文科省の「大学入学者選抜実施要項」(例年5月末ごろ各大学に通知)において｢推薦・AO入試｣での基礎学力の状況を把握する措置が求められている。
　23年度入試では、入学者約60万人のうち、｢推薦・AO入試｣入学者の割合(43.8％、約26.2万人)がやや減少し、学科試験主体の「一般入試」入学者の割合(55.7％、約33.4万人)が僅かながら増加している。特に国公立大ではセンター試験を課す｢推薦・AO入試｣の拡大傾向もみられる。(図9参照)

 

 

　こうした学校教育での学習状況や受験における入試状況の変化は、今後の児童・生徒の学習意欲の向上、基礎学力の定着などにも結びついていくものと期待される。