旺文社
教育情報センター

Educational Information Center

 

 

　教育の目的は、「人格の完成と平和で民主的な国家及び社会の形成者の育成」であるとされる(教育基本法第1条)。この目的は時代の変化に関わらず、普遍的なものといえる。
　他方、学習指導要領は、各学校において編成される教育課程の基準として国が定めるものである。学習指導要領はこれまで、上記のような教育の目的を実現すべく、社会や児童生徒の変化などを踏まえ、およそ10年に1度改訂されてきた。
　今回改訂された高等学校学習指導要領は21年3月に告示され、数学、理科及び理数(主に専門学科で開設)の各教科・科目は24年4月1日の入学生から学年進行で“先行実施”、全ての教科・科目は25年4月1日の入学生から学年進行で“全面実施”されている。

 

 

　学習指導要領(21年3月告示の高等学校学習指導要領。以下、同)では、育成すべき資質・能力の基本として「生きる力」の理念を継承し、「生きる力」を支える「確かな学力」(①基礎的な知識・技能／②それらを活用して課題を解決する思考力・判断力・表現力等／③学習意欲・態度)、「豊かな心」、「健やかな体」の調和を重視している。
　各学科に共通する各教科・科目については、国語(6科目)／地理歴史(6科目)／公民(3科目)／数学(6科目)／理科(10科目)／保健体育(2科目)／芸術(12科目)／外国語(英語：7科目)／家庭(3科目)／情報(2科目)の10教科57科目(旧課程：10教科59科目)となっている。
　卒業単位数などの教育課程編成に当たっての基本的な枠組みは、次のようになっている。
●　「卒業までに修得する単位数」は、「74単位」以上(旧課程と同様)。
●　全ての生徒に履修させる「必履修教科・科目」の最低合計単位数は、生徒の“多様性”と学びの“共通性”のバランスに配慮し、「31単位」としている(旧課程と同様)。
●　学習の基盤となる国語、数学、外国語(英語)における必履修科目については、全ての高校生が共通に履修する「共通必履修科目」(国語＝国語総合／数学＝数学Ⅰ／外国語＝コミュニケーション英語Ⅰ)を“新設”し、高校教育の共通性を高めている。
●　「週当たりの標準授業時数」(全日制)は「30単位時間」と旧課程と同様であるが、必要がある場合は増加することができることを明確化。
　なお、「年間授業週数」は「35週」を標準としている。各教科・科目の「1単位」は、1単位時間を50分として35単位時間の授業を標準としている(旧課程と同様)。

 

 

　今回の学習指導要領改訂における教育内容の主な改善としては、言語活動の充実／外国語活動の充実／伝統や文化に関する教育の充実／道徳教育の充実／体験活動の充実などとともに、理数教育の充実が図られている。
　理数教育の充実に関しては、近年の新しい科学的知見に対応する観点から指導内容を刷新している。
　例えば、理科では新しい生物学の内容として「遺伝情報とタンパク質の合成」を旧課程の「生物Ⅱ」(選択科目)から新課程の「生物基礎」(選択必履修科目)に移行したり、新課程「地学」(選択科目)の「膨張する宇宙」で現代の宇宙像を扱ったりするなど、学習内容の改新と充実を図っている。
　数学では、中学校で学習する「資料の活用」との接続や様々な事象を数学的に考察する能力を培う観点から、「統計」に関する内容(「データの分析」)を旧課程の「数学Ｂ」から、全ての高校生が共通に履修する共通必履修科目の「数学Ⅰ」に移行し必修化している。
　また、理科では科目履修の柔軟性を向上させたり、数学では学習の系統性と科目選択の多様性などに配慮したりするなどの内容・科目編成となっている。

 

 

 

　新しい学習指導要領では上述のように、卒業に必要な修得単位数や必履修教科・科目の単位数、週当たりの標準授業時数など教育課程編成の基本的枠組みは旧課程と同じである。そうした中で、理数教育の充実をはじめ、英語教育では標準的な単語数を1,300語から1,800語に増加(中学・高校合わせて2,200語から3,000語に増加)させ、授業は英語で指導することを基本とするなどの充実・強化を図っている。
　その結果、新課程では卒業に必要な修得単位数や授業時数の拡大がみられる。
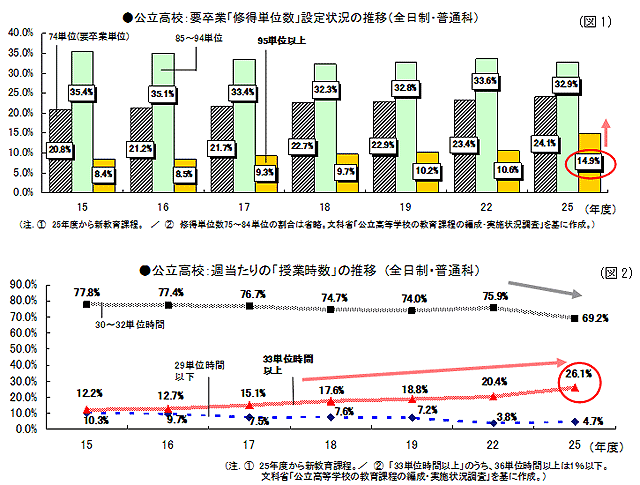
◆　要卒業「修得単位数」の拡大
　教育内容の充実によって、公立高校(全日制・普通科。以下、同)では、新課程において卒業までに修得する単位数が旧課程時に比べて増加の傾向を示している。
　25年度入学者の要卒業「修得単位数」の設定状況をみると、最低基準である「74単位」の設定が24.1％(調査対象の普通科数に占める割合。以下、同)／「85～94単位」の設定が32.9％／「95単位以上」の設定が14.9％となっている。
　これまでの要卒業「修得単位数」の推移をみると、「85～94単位」の設定が30％台で最も多いことに変わりないが、「95単位以上」の設定が年度を追って増加している中で、25年度は前回調査(旧課程)の22年度に比べ4.3ポイントの大幅な上昇である。(図1参照)
◆「授業時数」の増加
　週当たりの「授業時数」の設定状況をみると、標準の「30単位時間」を下回る割合は10％(調査対象の普通科数に占める割合。以下､同)以下で、最近は5％以下に低下している。
　週当たりの授業時数が最も多い設定は「30～32単位時間」の70％台であるが、25年度は70％を割っている。
　一方、「33単位以上」のタイトな設定は年度を追って増加しており、25年度は旧課程時の前回調査(22年度)に比べて5.7ポイント上昇の26.1％まで増加している。(図2参照)

 

＊　　　　　　　　＊　　　　　　　　＊

 

 

 

　新課程の数学は前述のように、生徒の多様化や中学校数学の内容等とのつながりを踏まえ、数学Ⅰを全ての高校生が履修する「共通必履修科目」としている。したがって、数学Ⅰは、全ての高校生に必要な数学的素養を習得するための内容によって構成されている。
　また、旧数学Ｃを廃止し、その内容を他科目に移行するなどして、数学Ａ(旧課程では全項目履修)と数学Ｂをそれぞれ3項目(分野)から2項目を選択履修する科目に再編した。
　新課程「数学」の科目編成は、旧課程の7科目から6科目に再編された。(表1参照)

 

 

　数学の今回の改訂では、ほとんどの科目は科目名や標準単位数を変えずに新しい項目(分野)を追加したり、履修方法を変えたりしている。ただ、数学における学習の深化や将来の進路への対応などから、単位数を増やして内容の充実を図った科目もある。
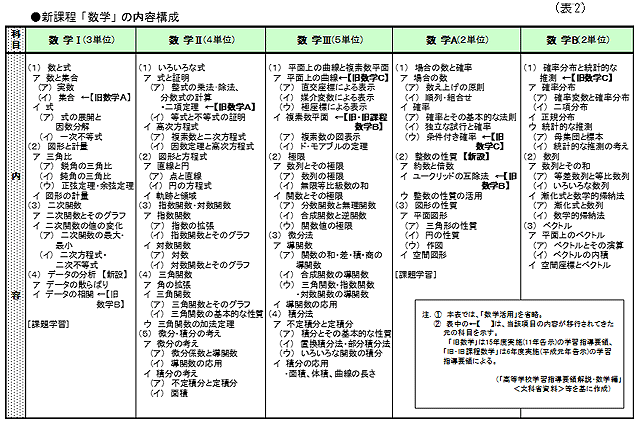
　各科目の主な内容や変更等については、およそ次のとおりである。(表2参照)
◆　数学Ⅰ(３単位)
　数学Ⅰは、中学校数学が「数と式｣、｢図形｣、｢関数｣、｢資料の活用」の4領域で構成されていることを踏まえ、次の内容で構成されている。
①　数と式　／　②　図形と計量　／　③　二次関数　／　④　データの分析
　なお、「課題学習」も内容に位置付けられている。
　新設された「データの分析」は中学校との接続に配慮しつつ、新しい内容として「四分位数」や「箱ひげ図」などを扱い、旧数学Ｂから移行された「分散｣、｢標準偏差｣、｢散布図｣、｢相関係数｣などとともに、データを整理・分析して傾向を把握するための基礎的な知識・技能の習得を目指している。
　標準単位数は3単位であるが、2単位までの減単は可能とされている。
●　中学校に移行した旧数学Ⅰの内容
　旧数学Ⅰに含まれていた次の内容は、中学校に移行された。
　数の集合と四則／二次方程式の解の公式／いろいろな事象と関数／相似形の面積比・体積比／球の表面積・体積
◆　数学Ⅱ(４単位)
　数学Ⅱの内容は旧数学Ａから移行された「二項定理」以外、旧課程と大きく変わらず、標準単位数も変わらない。数学Ⅱは数学Ⅰの内容を発展、拡充させるとともに、数学Ⅲへの学習の系統性を踏まえ、次の内容で構成されている。
①　いろいろな式　／　②　図形と方程式　／　③　指数関数・対数関数／
④　三角関数　／　⑤微分・積分の考え
◆　数学Ⅲ(５単位)
　数学Ⅲは、理数教育の充実といった今回の改訂趣旨を端的に示した科目のひとつといえよう。数学に強い興味・関心をもって更に深く学習しようとする生徒や、将来、数学が必要な専門分野に進もうとする生徒の履修に対応した科目として、標準単位数を旧数学Ⅲの3単位から5単位に増単され、内容も旧課程より拡充されて次のような内容で構成されている。
①　平面上の曲線と複素数平面　／　②　極限　／　③　微分法　／　④　積分法
　「平面上の曲線と複素数平面」は、旧数学Ｃの「式と曲線」の内容に加え、旧・旧課程(6年度実施<平成元年告示＞）の数学Ｂで扱われた「複素数平面」(｢複素数の図表示」と「ド・モアブルの定理」)を扱う。また、「平面上の曲線」で扱う曲線は、二次曲線やサイクロイド、アステロイドなど「微分法」や「積分法」でも扱われる曲線が中心となる。
　なお、｢極限｣、｢微分法｣、｢積分法」は旧課程とほぼ同じ扱いである。
◆　数学Ａ (２単位)
　数学Ａは、次のような内容で構成されている。また、数学Ⅰと同様、「課題学習」も内容に位置付けられている。
①　場合の数と確率　／　②　整数の性質　／　③　図形の性質
「場合の数と確率」では、「期待値」を数学Ｂの「確率変数と確率分布」に統合し、旧課程の旧数学Ｃ(今回の改訂で廃止)の内容であった「条件付き確率」がここで扱われる。
　「整数の性質」は、今回の改訂で新設された項目である。整数に関わる性質は小学校や中学校でも扱われているが、ここでは「ユークリッドの互除法」や「二元一次不定方程式」の整数解などが扱われる。
　「図形の性質」は、旧数学Ａの「平面図形」が拡充され、作図や空間図形も扱われる。
　旧課程の旧数学Ａ(2単位)は、“全項目履修”(平面図形、集合と論理、場合の数と確率)であったが、新課程の数学Ａは上記①～③の3項目から2項目の“選択履修”を標準とする。
◆　数学Ｂ (２単位)
　数学Ｂは、旧課程の旧数学Ｂの内容を一部引き継ぎ、次のような内容で構成されている。
①　確率分布と統計的な推測　／　②　数列　／　③　ベクトル
　「確率分布と統計的な推測」は、旧数学Ｃの「確率分布」と「統計処理」を統合・整理した内容である。
　ところで、旧数学Ｂは4項目(数列、ベクトル、統計とコンピュータ、数値計算とコンピュータ)の内容で構成され、「数列」と「ベクトル」の“選択履修”が主体であった。こうした選択項目の偏りを小さくするために、新課程の数学Ｂでは3つの内容で構成されている。
　ただ、3項目を履修するには3単位程度を要するため、生徒の実態や単位数等に応じて内容を適宜選択することとされ､新課程でも「数列」と「ベクトル」の選択履修が主体である。
＊　新課程「数学」では前述5科目のほか、「数学活用」(2単位)が設定されている。この科目は旧課程の「数学基礎」(2単位)の趣旨を生かし、内容を発展させた科目である。

 

 

 

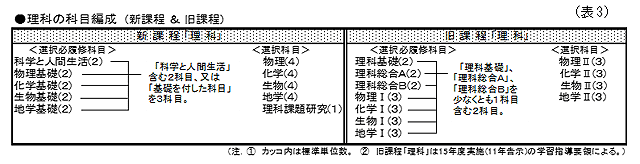
　新課程｢理科｣は、物理、化学、生物、地学の4領域のそれぞれが「基礎を付した科目」(以下、「基礎科目」。標準単位数：2単位)4科目と「基礎を付していない科目」(以下、「発展科目」。4単位)4科目に再編されたとともに、“総合科目”として「科学と人間生活」(2単位)及び「理科課題研究」(1単位)が新設され、計10科目となった。(表3参照)

 

 

　新課程「理科」の「選択必履修」は、「科学と人間生活」1科目及び「基礎科目」から1科目選択の計2科目履修、又は「基礎科目」から3科目を選択履修する。

 

　選択必履修方法の変更の背景には、学校現場での履修実態があるとみる。
　旧課程では、例えば、「理科総合Ａ」(物理・化学分野)と「生物Ⅰ」の2科目を選択することが適当であるとされ、この2科目を履修することで理科の“3領域”が履修できると構想されていた。
　しかし、学校現場では限られた授業時数における学習指導の効率化を図る観点などから、例えば、「理科総合Ａ」(物理・化学分野)と「物理Ⅰ」又は「化学Ⅰ」の2科目を選択させ、実質的には“2領域”の履修に留まるケースが少なくなかった。
　つまり、理系では物理・化学領域の履修を主体に、文系では「理科総合Ｂ」(生物・地学分野)と「生物Ⅰ」又は「化学Ⅰ」による生物・化学領域の履修が主体(「地学Ⅰ｣の履修は少ない)になっていた。
　新課程では、こうした実態も踏まえ、物理、化学、生物、地学の4領域から3領域以上を履修するという旧課程の“理念”を維持したうえで、学校の裁量を拡大し、生徒のニーズに応じた科目履修の柔軟性を高める観点から、3領域以上の科目を履修する場合には所謂“総合科目”(「科学と人間生活」)の履修を不要としている。(表3参照)

 

 

　理科教育については、科学的な概念理解など基礎的・基本的な知識・技能の確実な定着を図る観点から、「エネルギー」(物理)／「粒子」(化学)／「生命」(生物)／「地球」(地学)といった科学の基本的な見方や概念を柱として、小・中・高校を通じた理科の内容の構造化を図る方向で改善された。
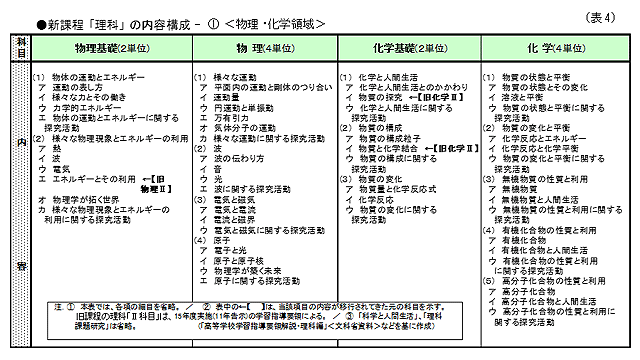
◆「基礎科目」
　「基礎科目｣は、旧課程の「Ⅰを付した科目」(Ⅰ科目)、「Ⅱを付した科目」(Ⅱ科目)のうち、中学と高校との接続を考慮しつつ、より基本的な内容で構成し、基本的な概念や探究方法を学習する科目として「物理基礎」／「化学基礎」／「生物基礎」／「地学基礎」で編成されている。
　「物理基礎」は物体の運動と力、物理現象とエネルギーなど／「化学基礎」は化学と人間生活、物質の構成、物質の変化など／「生物基礎」は細胞と遺伝子、生物の多様性と生態系など／「地学基礎」は宇宙における地球／変動する地球などで構成されている。
　また、｢基礎科目｣は旧｢Ⅰ科目」と旧｢Ⅱ科目」を含めて中学理科との接続を踏まえているため、旧｢Ⅱ科目」からの移行もみられる。
　例えば、「物理基礎｣の「エネルギーとその利用｣に、旧｢物理Ⅱ｣から「放射線及び原子力の利用とその安全性」が移行されたり、「化学基礎」の「物質と化学結合」(イオンとイオン結合、金属と金属結合、分子と共有結合)には旧｢化学Ⅱ」からの移行があったり、「生物基礎」では「遺伝子とその働き」（遺伝情報の配分、遺伝情報とタンパク質の合成）や「植生の多様性と分布」などに旧｢生物Ⅱ｣からの移行があるほか、「地学基礎」には「宇宙の構成」(宇宙のすがた)や「活動する地球」(プレートの運動)に旧｢地学Ⅱ」からの移行がある。
　なお、「基礎科目」は、観察・実験を重視するとともに、旧｢Ⅰ科目」と同様、各大項目に「探究活動」を位置付け、探究的な学習の推進を図っている。(表4・表5参照)
◆「発展科目」
　前述の「基礎科目」を基礎として、観察・実験などを行い、より高度な概念や探究方法を学習する「発展科目」として「物理」／「化学」／「生物」／「地学」が設置された。

　「物理」は運動、波、電気と磁気、物質と原子など／「化学」は物質の状態や変化と平衡、無機物質、有機化合物及び高分子化合物の性質と利用など／「生物」は生物現象と物質、生物の生活と反応、生物の集団、生物の進化など／「地学」は地球の概観、地球の活動と歴史、地球の大気と海洋、宇宙の構成などで構成されている。
　「発展科目」は、それぞれに対応する「基礎科目」を履修した後に履修する。

　また、旧課程では“選択項目”であった項目を“必修化”して、履修内容を充実させている。「発展科目｣において、旧「Ⅱ科目｣で選択項目であった項目が必修項目となった項目は、次のとおりである。
●　｢物理｣：「物質と原子」、「原子と原子核」の内容を整理、必修化（旧｢物理Ⅱ」で選択)
●　｢化学」：「生活と物質」、「生命と物質」の内容を整理、必修化（旧｢化学Ⅱ」で選択)
●　｢生物」：「生物の分類と進化」、「生物の集団」の内容を整理、必修化（旧｢生物Ⅱ」で選択)
●　｢地学」：「地球の探究」、「地球表層の探究」、「宇宙の探究」の内容を整理、必修化（旧｢地学Ⅱ」で選択)
　また、「発展科目」には「基礎科目」に引き続き、大項目に「探究活動」を新たに位置付け、探究的な学習の推進を図っている。(表4・表5参照)

 

 

＊　　　　　　　　＊　　　　　　　　＊

 

■　27年センター試験　：　新課程　「数学・理科」　実施概要　■
　27年センター試験の出題教科・科目及び出題範囲は、数学と理科については24年度から先行実施されている新しい学習指導要領(21年3月告示)に対応した出題となる。
　数学・理科以外の教科については旧課程対応(11年3月告示、15年度実施の高等学校学習指導要領)で実施される。
なお、数学・理科における旧課程履修者に対しては、「経過措置」(後述)が講じられる。
 
【数　学】

 

◆　出題科目：｢数学Ⅰ」／「数学Ⅰ・数学Ａ」／「数学Ⅱ」／「数学Ⅱ・数学Ｂ」(4科目)

◆　出題範囲：「数学Ⅰ」は「数学Ⅰ」の全て。／「数学Ⅰ・数学Ａ」は「数学Ⅰ」及び「数学Ａ」の全て。／「数学Ⅱ」は「数学Ⅱ」の全て。／「数学Ⅱ・数学Ｂ」は「数学Ⅱ」及び「数学Ｂ」の全て。
◆　特記事項
●　「数学Ａ」については、3項目の内容(場合の数と確率／整数の性質／図形の性質）のうち、2項目以上を履修した者に対応した出題となり、問題を“選択解答”する。
●　「数学Ｂ」については、3項目の内容(確率分布と統計的な推測／数列／ベクトル）のうち、2項目以上を履修した者に対応した出題となり、問題を“選択解答”する。

 

 

　数学の出題科目は次の2グループで、それぞれのグループから1科目を選択解答する。
●　①グループ：「数学Ⅰ」／「数学Ⅰ・数学Ａ」(１科目選択；3単位又は5単位相当)
●　②グループ：「数学Ⅱ」／「数学Ⅱ・数学Ｂ」(１科目選択；4単位又は6単位相当)
●　数学の②グループには、数学2科目のほか、「専門学科に関する科目」として「工業数理基礎」、「簿記・会計」、「情報関係基礎」の3科目が配置されており、　合計5科目から1科目を選択解答する。「専門学科に関する科目」は旧課程(11年3月告示の高等学校学習指導要領)対応の出題である。なお、全教科・科目が新課程対応となる28年センター試験では、出題科目から「工業数理基礎」が除外される。

 

 

　数学の問題冊子は、①グループ及び②グループそれぞれにおいて、新・旧課程科目を含む合冊となる。
●　数学①の問題冊子＝「数学Ⅰ」「数学Ⅰ・数学Ａ」及び「旧数学Ⅰ」「旧数学Ⅰ・旧数学Ａ」
●　数学②の問題冊子＝「数学Ⅱ」「数学Ⅱ・数学Ｂ」及び「旧数学Ⅱ・旧数学Ｂ」(「旧数学Ⅱ」の経過措置は講じられない)

 

 

●　事前登録：センター試験に出願する際、数学を「受験する」か「受験しない」か、受験の有無を志願票で「事前登録」する。
センター試験を受験するに当たっては、数学に限らず、受験教科(国語、地理歴史、公民＜出願時には「地理歴史、公民」を１教科として登録＞、数学、理科、外国語)／地理歴史、公民の科目数／理科の科目選択方法／数学②及び外国語の「別冊試験問題」の配付希望を事前登録する。
登録内容の変更は「確認はがき」で確認後、｢登録教科等訂正届｣を指定期日までに大学入試センターに郵送する。
●　数学を受験登録した場合、試験当日は「数学①のみ」、「数学①＋数学②」、「数学②のみ」の受験が可能である。
●　新課程履修者は、旧教育課程による出題科目(「旧数学Ⅰ」「旧数学Ⅰ・旧数学Ａ」「旧数学Ⅱ・旧数学Ｂ」)を選択解答できない。
●　旧課程履修者は、新課程・旧課程科目を含め、数学①では4科目から1科目を、数学②では3科目から1科目をそれぞれ選択解答できる。
 
【理　科】

 

◆　出題科目：「物理基礎」／「化学基礎」／「生物基礎」／「地学基礎」／「物理」／「化学」／「生物」／「地学」(8科目)
◆　出題範囲：上記 8科目において、それぞれの科目構成の内容の全てが出題範囲となる。

 

 

　理科の出題科目は次の2グループに配置され、①グループ及び②グループから最大3科目を選択する。具体的には、次のA～Dの4つのパターンから選択解答する。
●①グループ：「物理基礎」／「化学基礎」／「生物基礎」／「地学基礎」
●②グループ：「物理」／「化学」／「生物」／「地学」
◎　“４パターン”(Ａ～Ｄ)別の選択解答方法

◆　特記事項
●　「発展科目」の「物理」、「化学」、「生物」、「地学」については、旧課程で“選択履修”であった項目が“必修化”されたが、高校の教育課程の現状を踏まえて受験者の大幅な負担増にならないよう、“一部に選択問題”が配置される。
●　①グループについては、“1科目のみの受験は認められない”。
●　②グループの試験時間において2

　科目を選択する場合、解答順に「第1解答科目」及び「第2解答科目」に区分して各60分間で解答する。「第1解答科目」と「第2解答科目」の間に答案回収等のための時間を設け、それらの合計時間(130分)を試験時間とする。
●　理科の受験科目の選択解答方法(A～D)は、出願時に申し出る(事前登録。後述)。
●　選択解答方法Cにおける「基礎科目」と「発展科目」の組合せで、同一名称を含む科目同士の選択については制限されず、同一名称を含む科目同士の選択は可能である。
　ただし、センター試験を利用する大学(学部)によっては､「基礎科目」と「発展科目」における同一名称を含む科目の組合せを不可としているところがある。
“同一名称を含む科目の組合せ”は、「物理基礎」と「物理」／「化学基礎」と「化学」／「生物基礎」と「生物」／「地学基礎」と「地学」。
なお、地理歴史と公民では、同一名称を含む科目の組合せで2科目選択はできない。

 

 

　理科の問題冊子は､次のように「基礎科目」「発展科目」「旧課程科目」別の3分冊になる。
●　理科①の問題冊子＝基礎科目用：「物理基礎」「化学基礎」「生物基礎」「地学基礎」
●　理科②の問題冊子＝新課程用：「物理」「化学」「生物」「地学」旧課程用：「理科総合Ａ」「理科総合Ｂ」「物理Ⅰ」「化学Ⅰ」「生物Ⅰ」「地学Ⅰ」
●　理科②では、問題冊子を新課程用、旧課程用いずれか1冊を配付する。

 

 

●　理科を受験する場合、「“新課程科目”を受験する」(新課程履修者及び旧課程履修者)のか、「“旧課程科目”を受験する」(旧課程履修者のみ)のかを事前登録する。
●　“新課程科目”を受験する場合：Ａ～Ｄの4パターンのうちから1つを事前登録する。
●　“旧課程科目”を受験する場合：旧課程履修者で理科②の旧課程「理科｣を受験する場合、「“１科目”受験」なのか、「“２科目”受験」なのかを事前登録する。
●　試験当日、登録した「科目選択方法」を変更することはできない。
●　理科①(基礎科目)は解答時間60分で、「基礎4科目」から必ず“2科目”を選択解答する。2科目の解答の順序、及び時間配分は自由。また、「解答用紙」は1枚で、表面に“2科目分”を解答する。
●　旧課程履修者は、理科の旧課程科目と新課程科目を組み合せた選択解答はできない。
　なお、数学では、旧課程履修者は旧課程科目と新課程科目を組み合せた選択解答が可能である。
●　数学を新課程(又は旧課程)科目、理科を旧課程(又は新課程)科目(いずれも事前登録)の組合せで受験することもできる。

 

 

　27年センター試験の出題教科・科目は、数学・理科の新課程対応による6教科・31科目に｢経過措置｣(後述)の旧課程「数学・理科」の9科目が加わり､合計40科目の過去最多となる。試験日程(本試)は、27年1月17日(土)及び18日(日)の両日、次の時間割で実施される。(表6参照)

 

 

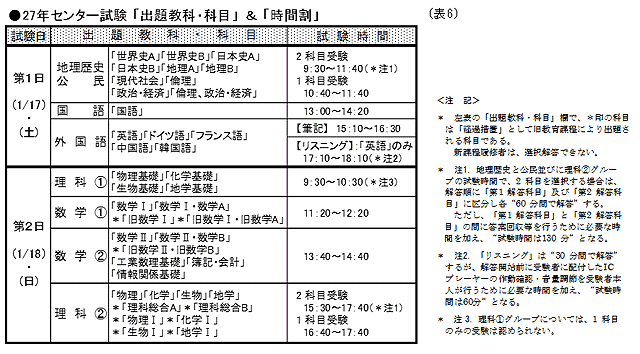
　27年センター試験「理科」は前述したように、理科①と理科②の試験枠で第2日目(27年1月18日)に実施される。
　その「試験時間割」と「受験方法」は、両試験枠における新課程「理科」の「パターン別選択解答」、理科②における新・旧課程「理科」の「1科目選択解答」と「2科目選択解答」など、従前に比べて大幅に変更される。
　理科①と理科②の「時間割」と「受験方法」などの概要を改めて図にまとめると、次のようになる。(図3参照)

 

 

 

 

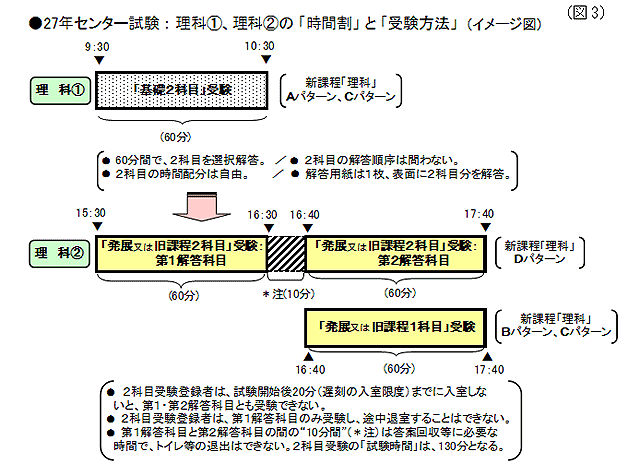
　27年センター試験では、新課程の数学と理科が24年度から先行実施されたことに伴い、この2 教科に関しては新課程対応で、その他の教科については旧課程対応で実施される。
　このため、数学と理科に関し、27年センター試験の全ての受験者は、新課程対応の試験を受けるのが原則であるが、旧課程履修者(24年3月以前の高校入学者など)に対しては次のような「経過措置」が講じられる。旧課程履修者のうち希望者は、「経過措置」による受験が可能である。数学・理科の｢経過措置｣は、27年センター試験に限り講じられる。

 

 

　旧課程に基づく「数学Ⅰ」、「数学Ⅰ・数学Ａ」、「数学Ⅱ・数学Ｂ」、「理科総合Ａ」、「理科総合Ｂ」、「物理Ⅰ」、「化学Ⅰ」、「生物Ⅰ」、「地学Ⅰ」は、旧課程履修者のための出題科目として残され、従前と同様の試験時間・配点により出題される。「経過措置」の出題方法、科目選択の方法等は、下表のとおりである。(表7参照)
　なお、新課程履修者(数学・理科)＜24年4月高校入学、27年3月卒業見込み等で、新課程「数学・理科」履修者＞は、旧課程対応の出題科目を選択解答できない。

 

 

 

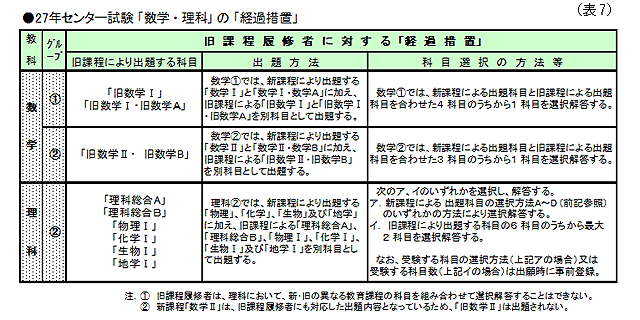
　27年センター試験(本試)では、次の各科目間で原則として“20点以上”の平均点差が生じ、これが“試験問題の難易差”に基づくものと認められる場合に「得点調整」が行われる。ただし、受験者数が“1万人未満の科目”は、得点調整の対象外とされている。
◆　27年センター試験「得点調整」の対象
●　地理歴史の「世界史Ｂ」､「日本史Ｂ」､「地理Ｂ」の間
●　公民の「現代社会」､「倫理」､「政治・経済」の間
●　数学①の「数学Ⅰ・数学Ａ」と「旧数学Ⅰ・旧数学Ａ」の間
●　数学②の「数学Ⅱ・数学Ｂ」と「旧数学Ⅱ・旧数学Ｂ」の間
●　理科②の「物理」､「化学」､「生物」､「地学」､
「物理Ⅰ」､「化学Ⅰ」､「生物Ⅰ」､「地学Ⅰ」の間

 

 

　得点調整が廃止された“旧・旧課程”対応初年度の9年センター試験は、約10万人の既卒者が受験した｢旧数学Ⅱ｣(平均点42.21点)と、約25万人の現役生等(既卒者も受験可)が受験した当時の新課程｢数学Ⅱ・Ｂ」(同63.90点)の平均点差は21.69点と、大幅に開いた。この平均点差は社会的な波紋を呼び、当時の文部省は大学に2段階選抜の原則中止を要請。
　大学入試センターはこうした事態を踏まえ、10年センター試験(経過措置は9年・10年実施)では数学の｢経過措置｣科目も含めた得点調整の復活を決めた。
27年の「経過措置」科目を含めた「得点調整｣の背景には、こうした経緯がある。

 

＊　　　　　　　　＊　　　　　　　　＊

 

 

 

　旧学習指導要領(小・中学校10年12月、高校11年3月改正告示)は、中教審の第1次答申『21世紀を展望した我が国の教育の在り方について』(8年7月)を踏まえ、14年度からの完全学校週5日制の下、“ゆとり”の中で「生きる力」の育成を基本として、小・中学校では14年度から、高校では15年度から学年進行で全面実施された。
　旧課程では、小・中学校での学習内容が3割削減され、高校でも要卒業単位数が「80単位」以上から「74単位｣以上に、必履修単位数が「38単位」以上から「31単位」以上に削減されるなど、学習内容や授業時数、履修科目の縮減が図られた。
　その結果、平成10年代は“学力低下論”が社会的にも大きな波紋を広げ、“ゆとり”か“詰め込み”かといった二項対立的な議論がみられた。
　このような経緯を踏まえ、現行の学習指導要領では前述したように「生きる力」の理念を継承するとともに、小・中学校では授業時数を増やして学習内容を拡充させ、高校では履修内容の充実と履修科目の再編を図るなど、“脱・ゆとり教育”へと大きく舵を切った。
　特に理数教育については、算数・数学の授業時数を小学校16％増、中学校22％増／理科の授業時数を小学校16％増、中学校33％増とし、数量・図形の知識・技能を実際の場面で活用する能力の育成や観察・実験等の充実・時間の確保を図っている。
　高校では前述のように要卒業単位数や必履修単位数などの規定単位数は旧課程と同じであるが、公立高校(全日制・普通科)での要卒業単位数や週当たりの授業時数の設定は増加しており、中学校との接続に配慮した項目の配置や履修科目の再編など、指導内容の充実と刷新が図られている。
　こうしたことから、27年センター試験は、いわば“脱・ゆとり教育”から生まれた新課程「数学・理科」の最初の共通テストとして注目される。

 

 

　センター試験の出題教科・科目は、・大学入学志願者の高等学校段階の学力を客観的に把握すること／・大学での個別試験との組合せ等で個性・特色に応じた多様な入学者選抜の実施に資すること／・高校教育の「共通性」(必要最低限の知識・技能、教養等の確保)と「多様性」(学校の裁量や生徒の選択の弾力化等)のバランスに配慮している学習指導要領を踏まえ、必履修教科・科目を尊重しつつ、大学進学希望者の学習意欲を含めた学力の育成に資することなどの観点から決定される。
　こうした観点から、新課程「理科」のセンター試験は、「基礎4科目」と「発展４科目」の計8科目を4パターンに区分した選択解答方式が導入された。
科目数も含めた“4パターン”別の選択解答方式を導入した背景には、物理・化学・生物・地学の4領域中、3領域以上履修を基本理念とする新課程のカリキュラム編成や、｢基礎科目｣と｢発展科目｣の履修内容や標準単位数等を踏まえ、新課程｢理科｣の改訂趣旨を活かしつつ、センター試験利用大学(学部)における広範な科目選択に応える狙いがあったとみられる。
　ただ、パターン別の選択解答方式は、「基礎科目」と「発展科目」枠別の“科目選択”と、その“選択科目数”がセットになり、これに理科４領域の“領域(科目分野)選択”が加わる。さらに、大学志願者の大学・学部選択(併願)の範囲を狭めないよう大学の｢基礎科目｣指定においても｢発展科目｣受験者に個別試験の受験資格を付与する所謂「みなし措置」(得点換算もあり得る)の導入など、センター試験｢理科｣の利活用は極めて複雑化している。

 

 

　センター試験｢理科｣のパターン別の選択解答方式は、上記のような複雑化の一方で、大学(学部)の科目指定(科目選択等の利用)方法の“類型化”と、センター試験｢理科｣の“機能的分化”をもたらしたといえる。
　これまでは、複数の「理科」試験枠内に配置された出題科目からそれぞれ1科目、あるいは1つに統合された試験枠(24年度～26年度)から最大2科目の選択解答方式であった。
　他方、Ａ～Ｄの“4パターン”に配置された科目から、それぞれの選択方法に則って選択解答するパターン別の選択解答方式では、大学(学部)のセンター試験｢理科｣科目指定の類型化が図られ、結果的にセンター試験｢理科｣の機能別分化(基礎科目：日常生活・社会との関連重視、定性的／発展科目：基礎科目の深化、発展的・定量的)につながっている。
　因みに、27年センター試験「理科｣の国公立大における指定(利用)科目のおおよその傾向をみると、文系ではＡパターン(基礎2科目)又はＢパターン(発展1科目)が最も多く、理系ではＤパターン(発展2科目)を主体としてＣパターン(基礎2科目＋発展1科目)など、さまざまな選択パターンを指定している。

 

 

　センター試験の新課程｢理科｣は、学習指導要領の趣旨を活かしつつ、高校教育や大学志願者の多様性に応えているとはいえ、その利活用は前述のように極めて複雑である。
　ところで現在、中教審では国レベルで実施する“共通テスト”として、「達成度テスト」(基礎レベル・発展レベル：仮称)を検討、議論している。
“基礎レベル”は高校生の基礎学力の保証と学習の改善を目的に、高校教育の共通性とその質を担保するテストといえる。“発展レベル”は学生の主体的な学びと考える力の向上を図ることなどを目的に、大学入学者選抜の改善策のひとつとして構想されている。
　そこで現行の学習指導要領を前提とするならば、「達成度テスト・基礎レベル」(仮称)では中学｢理科｣とのつながりなどを考慮し、例えば、センター試験｢理科｣の「基礎科目」を「物質・エネルギー基礎」(仮称)と「生命・地球基礎」(仮称)の2科目、つまり物理・化学系と生物・地学系の2領域に“合科目”化したらどうか。
　また、センター試験の代替として構想されている「達成度テスト・発展レベル」(仮称)については、6教科・31科目(27年は｢経過措置｣科目を含めると40科目)にも及ぶ現行のセンター試験の出題教科・科目を踏襲するのではなく、“合教科・科目”化などによる出題教科・科目の再編・統合、出題科目数の縮減、実施方法の簡素化などを図るべきである。